Navigation
A. Introduction & Setup
In this final project, you will be exploring various applications of Tries.
Pull the project skeleton from Github.
git pull skeleton masterB. The Trie
Implementation
In Trie.java, implement a Trie as we covered in lecture in any way you wish. It must implement the following two methods:
public boolean find(String s, boolean isFullWord) {
}
public void insert(String s) {
}And it must support Strings consisting of any sequence of char.
Given some word s of length N, insert should add s to the Trie in O(N) time and space. Note that, for comparison, adding all prefixes of a String of length N to a hash table takes expected O(N^2) time and space.
Given some query String s of length N, find whether or not the query String is in the Trie in O(N) time. If isFullWord is false, then partial prefix matches should return true; if isFullWord is true, then only full word matches should return true.
For example, given the following main method:
public static void main(String[] args) {
Trie t = new Trie();
t.insert("hello");
t.insert("hey");
t.insert("goodbye");
System.out.println(t.find("hell", false));
System.out.println(t.find("hello", true));
System.out.println(t.find("good", false));
System.out.println(t.find("bye", false));
System.out.println(t.find("heyy", false));
System.out.println(t.find("hell", true));
}We should expect to see this as output when the program is run:
true
true
true
false
false
falseError Cases
In your Trie class, throw an IllegalArgumentException when:
- A null or empty string is added. Null and empty strings by definition are never in the Trie.
AlphabetSort
As an example use of Tries, consider the following problem:
You are constructing a large dictionary for another language that uses some non-English alphabet. You want this dictionary to be ordered in the same way the foreign alphabet is ordered. This dictionary is very large, and you don't want to use a O(NM log N) time comparison-based sorting algorithm (where N is the number of words and M is the max length of the words).
AlphabetSort sorts a list of words into alphabetical order, according to a given permutation of some alphabet. It takes input from stdin and prints to stdout. The first line of input is some alphabet permutation. The remaining lines are the words to be sorted. If an input word has a character that is not in the alphabet, ignore that word. The output should be the sorted words, each on its own line, printed to stdout. The runtime should be linear in the length of the file: if the longest word is of length M and we have N words then it should run in time O(MN).
For example: given some input file called test.in with the following content:
agdbecfhijklmnopqrsty
hello
goodbye
goodday
deathWe should expect to see this as output when the program is run with test.in.
To use test.in as the input file, we use input redirection, linking stdin to a file descriptor:
$ java AlphabetSort < test.inExpected output:
goodday
goodbye
death
helloNOTE: "goodday" is before "goodbye" because in the specified ordering of the alphabet, "d" comes before "b". Both "goodday" and "goodbye" are before "death" and "hello" because "g" comes before either "d" or "h" in the specified ordering of the alphabet.
Warning: Do not use the StdIn class from the Princeton Standard Library. It's buggy and you might fail the autograder.
Error Cases
In your AlphabetSort class, throw an IllegalArgumentException when:
- No words or alphabet are given.
- A letter appears multiple times in the alphabet.
C. Autocomplete
Description
Autocompletion is an extremely common feature amongst software. Use cases range from web search to text editors; as a result, string algorithms are fairly well studied.
In this part, you will implement an immutable data type that provides autocomplete functionality for a given set of terms and weights. You will implement the following API:
public class Autocomplete {
/**
* Initializes required data structures from parallel arrays.
* @param terms Array of terms.
* @param weights Array of weights.
*/
public Autocomplete(String[] terms, double[] weights) {
}
/**
* Find the weight of a given term. If it is not in the dictionary,
* return 0.0.
*/
public double weightOf(String term) {
}
/**
* Return the top match for given prefix, or null if there is no
* matching term.
* @param prefix Input prefix to match against.
* @return Best (highest weight) matching string in the dictionary.
*/
public String topMatch(String prefix) {
}
/**
* Returns the top k matching terms (in descending order of weight)
* as an iterable.
* If there are less than k matches, return all the matching terms.
*/
public Iterable<String> topMatches(String prefix, int k) {
}
}Your algorithm should have a best case runtime that is much less than the number of matching prefixes.
Put more formally, let Np be the number of terms that match a query prefix p. For a best case input, your program should consider fewer than Np weights when collecting the top k matches. What constitutes a best case input depends on your implementation. Put another way, your algorithm should not have the property that it always examines all Np prefix matches.
Basically what this means is that your code shouldn't be checking every possible match for some prefix. You will be graded on runtime.
Your constructor should run in O(nm) time where n is the number of terms and m is the max length of the input terms.
It is up to you to decide which data structures and algorithms to design and use. The final subsection describes one sample effective strategy. You don't have to use it if you think your design will also meet the runtime requirements.
There is one caveat though: any data structures or libraries you use must come from the Java Standard Library; if it does not have something you need, write your own.
Input format
We provide a number of sample input files for testing. Each file consists of an integer N followed by N pairs of terms and positive weights. There is one pair per line, with the weight and term separated by a tab. The terms can be arbitrary strings consisting of Unicode characters, including spaces (but not tabs or new lines).
The file wikitionary.txt contains the 10,000 most common words in Project Gutenberg along with weights equal to their frequencies. The file cities.txt contains nearly 100,000 cities along with weights equal to their populations.
Input parsing is given to you in the form of a command-line test client in the skeleton code.
Your task
Implement Autocomplete.java to conform to the above runtime requirements. The skeleton gives the interface you must implement, along with a test client for your testing convenience.
You may break ties arbitrarily for this and the following part.
Here are a few sample executions of the test client that are also reflected in the autograder:
$ java Autocomplete wiktionary.txt 5
auto
6197.0 automobile
4250.0 automatic
comp
133159.0 company
78039.8 complete
60384.9 companion
52050.3 completely
44817.7 comply
the
56271872.0 the
3340398.0 they
2820265.0 their
2509917.0 them
1961200.0 there
$ java Autocomplete cities.txt 7
M
12691836.0 Mumbai, India
12294193.0 Mexico City, Distrito Federal, Mexico
10444527.0 Manila, Philippines
10381222.0 Moscow, Russia
3730206.0 Melbourne, Victoria, Australia
3268513.0 Montreal, Quebec, Canada
3255944.0 Madrid, Spain
Al M
431052.0 Al Mahallah al Kubra, Egypt
420195.0 Al Mansurah, Egypt
290802.0 Al Mubarraz, Saudi Arabia
258132.0 Al Mukalla, Yemen
227150.0 Al Minya, Egypt
128297.0 Al Manaqil, Sudan
99357.0 Al Matariyah, EgyptError Cases
There are several cases in which you should throw an IllegalArgumentException:
- The length of the terms and weights arrays are different
- There are duplicate input terms
- There are negative weights
- Trying to find the k top matches for non-positive k.
Sample Approach
Here, we will suggest one strategy that combines a Ternary Search Trie with a priority queue. The ternary search trie (TST) contains all of the terms, along with their weights. In addition, each node stores the maximum weight of its subtries - we will exploit this auxiliary information when we implement the search algorithm. You do not have to use this approach. An augmented trie can also work, depending on implementation details.
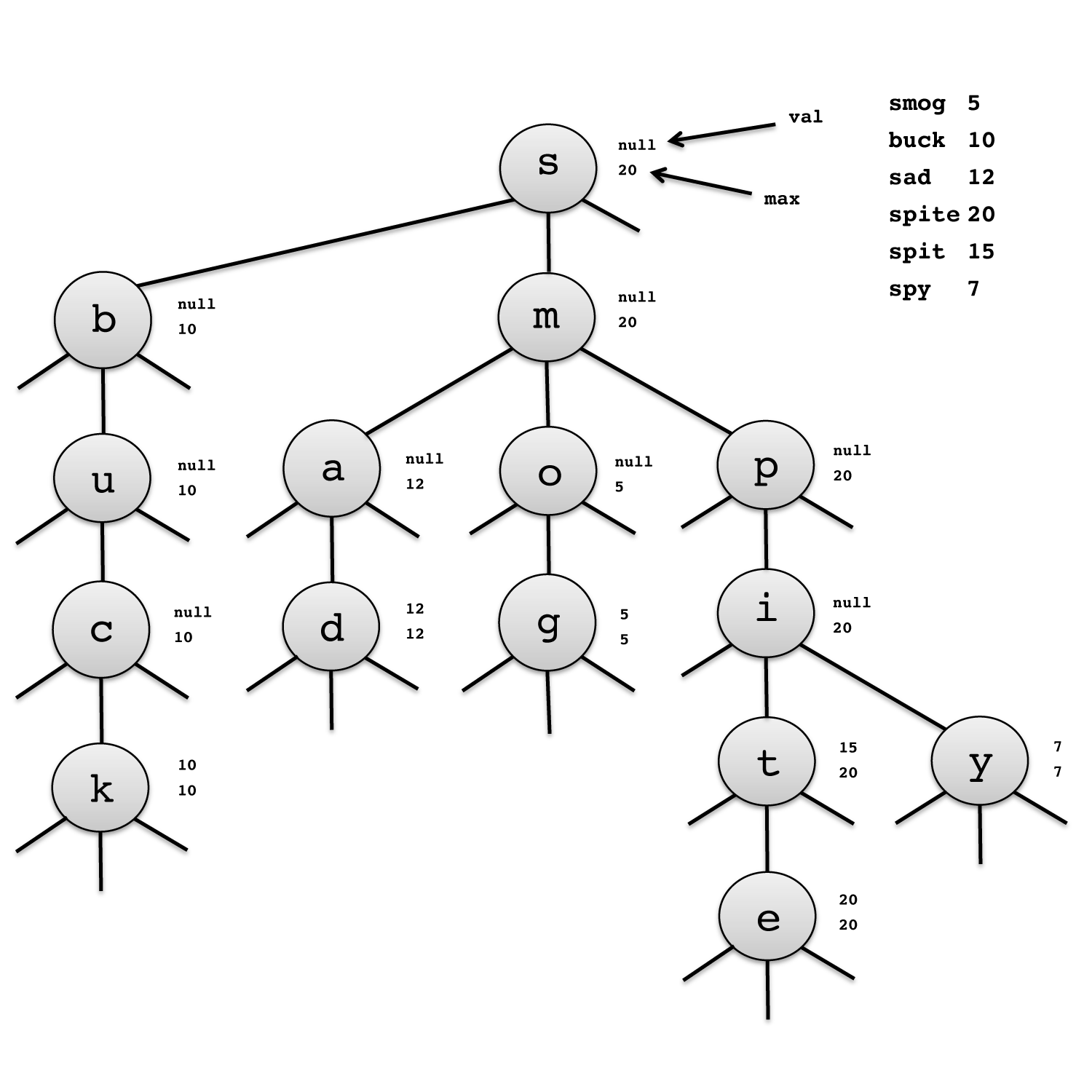
NOTE: A TST does not store words in the same way as a Trie! For example, the word "sbuck" is not in this TST (it's not a word in the first place!).
The TST shown above contains the words "smog", "buck", "sad", "spite", "spit", and "spy". In our implementation, we've essentially "reached" a word when we see that a weight has been set for it (e.g. at "k" on the left bottom node for the word "buck", the weight is set to 10.
If a given prefix matches some node's character, we can descend into that node's middle subtrie. If not, we look either to the left or right subtrie, depending on whether or not the character comes before or after the node. For example, for the word "buck", since "b" doesn't match "s", we look to the left subtrie because "b" < "s" and find "b".
For the word "sad", we first match with "s", then see that "a" < "m", so we descend into the left subtrie of the "m" node.
For our problem, we need to find the top k terms among those that start with a given prefix. All of the matching words are in the subtrie corresponding to the prefix, so the first step is to search for this node, say x. Now, to identify the top k matches, we could examine every node in the subtrie rooted at x, but this takes too long if the subtrie is large. Instead, we will use the weight of the node and the maximum weight of its subtries to avoid exploration of useless parts of the subtrie.
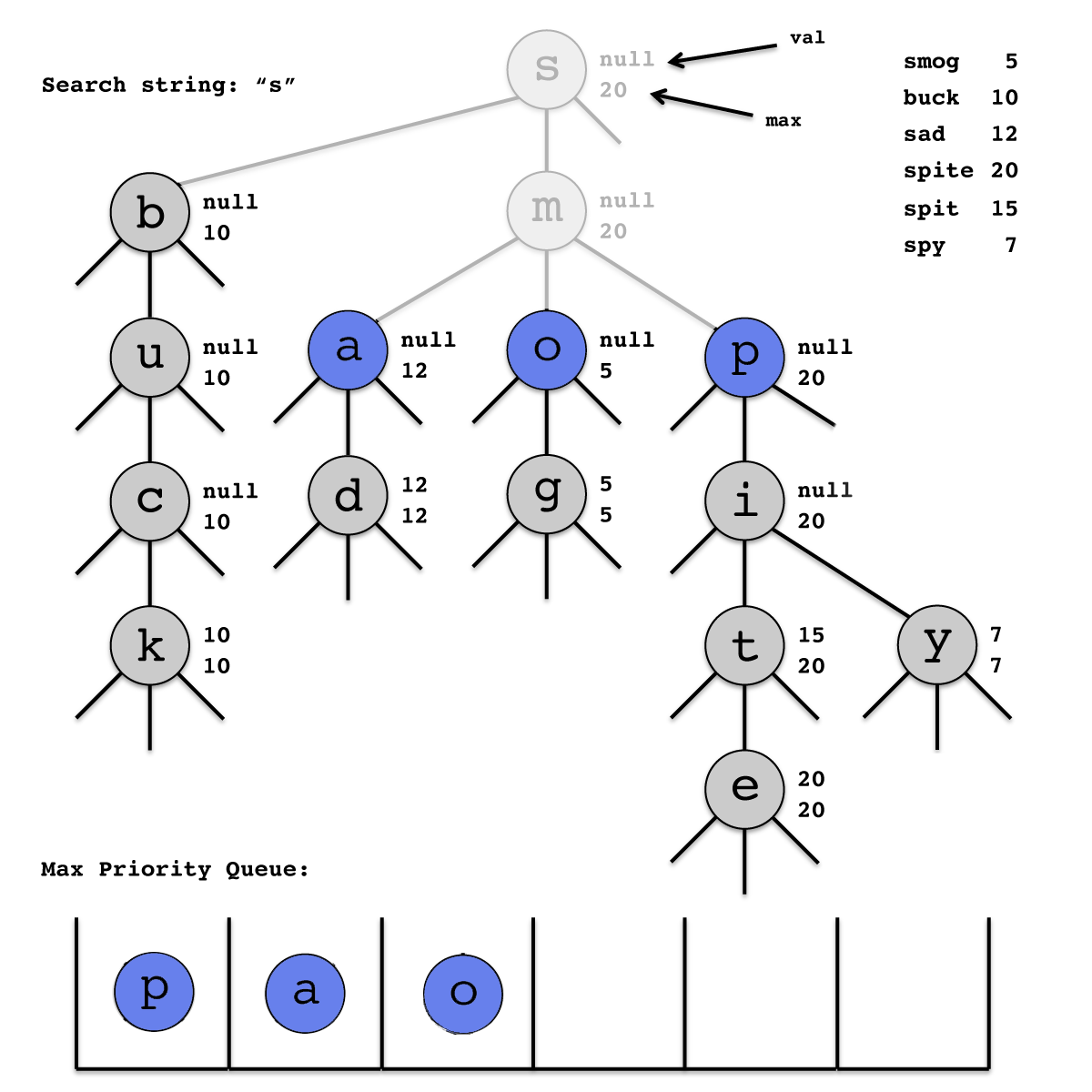
Edit (5/1/2015) - fixed hideous sentence! Specifically, we execute a modified tree traversal on the TST where we use a priority queue (instead of a stack for DFS or queue for BFS) pq that is maximally-oriented on the heaviest reachable node and we keep track of a Collection bestAnswer of the k highest weighted prefix-matching terms seen so far.
We can terminate the search as soon as the weight of the heaviest reachable node in the priority queue pq is less than or equal to the weight of the kth heaviest term in the Collection bestAnswer, because no remaining term in the subtrie has weight larger than the weight of the heaviest node in pq.
Below is a snapshot of the algorithm when searching for the top 3 terms that start with the prefix "s". The next node to be examined is the one containing the letter "p". The first matching term that is discovered will be "spit", followed by "spite", and "sad". The subtries rooted at "y" and "o" will never be explored.
Interactive GUI
Interactive GUI (optional, but fun and no extra work). Compile AutocompleteGUI.java. The program takes the name of a file and an integer k as command-line arguments and provides a GUI for the user to enter queries. It presents the top k matching terms in real time. When the user selects a term, the GUI opens up the results from a Google search for that term in a browser.
Spell Checking (Gold Points)
Implement the spellCheck function in Autocomplete.java:
/**
* Returns the highest weighted matches within k edit distance of the word.
* If the word is in the dictionary, then return an empty list.
* @param word The word to spell-check
* @param dist Maximum edit distance to search
* @param k Number of results to return
* @return Iterable in descending weight order of the matches
*/
public Iterable<String> spellCheck(String word, int dist, int k) {
}spellCheck() returns the highest weighted matches within d (less than our equal to d) edit distance of the word. Essentially, edit distance is the number of edits (deletions, insertions and replacements) that need to be made in order to change one word to another word. If the word is in the dictionary, then return an empty list.
Your implementation must be efficient. That is, it should run in better than brute-force time in the average case for large dictionaries (we will be testing it for runtime along with correctness). To be more specific, your program should not examine terms that are greater than edit distance d+1 from any prefix of the input word, and it should not repeat any computation that can be memoized. Outlined below is an efficient-enough solution to the dictionary edit distance problem that builds on your solution for part 1. You are free to use faster solutions, like DAWGs or BK-trees.
First, read the wikipedia article on Levenshtein distance. To make testing (and your implementation job!) easier this will be the only metric we use and test to determine edit distance; however if you are interested, feel free to look at edit distances that include transposition and phonetic matching algorithms that are widely used in search today. You can implement these on your own if you are interested. However do not submit them!
Take particular note of the two-row solution. We will optimize that using a trie. Think about the matrix we construct as we iterate through. As the index in the word increases, only the last row of the matrix changes. We can avoid a lot of work if we can process the words in order, so we never need to repeat a row for the same prefix of letters.
For example, suppose our query word is joshhug, but the closest match in our dictionary is boshbug. Then when comparing joshhug against boshbug, the rows will look like this:
String | Array
----------------------------------
| [0, 1, 2, 3, 4, 5, 6, 7]
b | [1, 1, 2, 3, 4, 5, 6, 7]
bo | [2, 2, 1, 2, 3, 4, 5, 6]
bos | [3, 3, 2, 1, 2, 3, 4, 5]
bosh | [4, 4, 3, 2, 1, 2, 3, 4]
boshb | [5, 5, 4, 3, 2, 2, 3, 4]
boshbu | [6, 6, 5, 4, 3, 3, 2, 3]
boshbug | [7, 7, 6, 5, 4, 4, 3, 2]Don't worry about the cases of characters. Uppercase and lowercase versions of the same letter will be treated differently.
For example, running an interactive spellcheck loop (by modifying the test client given in Autocomplete) showing the top 5 matches on wiktionary.txt of edit distance 1 gives:
whut
1605908.0 what
67063.6 shut
21374.0 hut
4155.8 whit
what
efect
148795.0 effect
20818.7 defect
16929.4 erect
13700.0 elect
heyy
gurl
262689.0 girl
4194.6 curlError Cases
For spellCheck, throw an IllegalArgumentException if dist is not positive, or if k is negative.
D. "Boggle" (Gold Points)
Description
The game of Boggle involves finding valid words on a 4x4 board of letters.
A brief description of the rules: Each player searches for words that can be constructed from the letters of sequentially adjacent cubes, where "adjacent" cubes are those horizontally, vertically, and diagonally neighboring. Words must be at least three letters long, may include singular and plural (or other derived forms) separately, but may not use the same letter cube more than once per word.
In this final part of the project, you will implement a generalized Boggle solver with a few modifications:
- You will not have to account for the "qu" tile
- You must support rectangular boards of arbitrary dimensions
The design choice of data structures and algorithms is up to you. However, we will impose a runtime requirement: you cannot inspect all possible permutations of words (in other words, you cannot submit a brute force solution). However, if your solution utilizes pruning, it will be sufficient. Also, as a warning: if you have a recursive solution, it is likely that it is slower by a nontrivial constant factor than an equivalent iterative solution.
Boggle reads an NxM newline separated letter grid from stdin, where the dimensions of the board (N and M) are given by the size of the input, unless the -r option is provided, in which case you should generate a NxM random board, where the characters are selected uniformly at random from the lowercase English alphabet and N and M can be specified by command line options.
The -n and -m arguments specify the size of the board if randomly generating one. The default values, if not given, are N=4 and M=4.
The -d option takes a file path to a newline separated dictionary. Otherwise, use the default dictionary, the file words in the current directory. This is provided in the skeleton. This file can also be found, on most Unix machines, in /usr/share/dict/words.
Prints the K longest unique words, where K=1 by default, and can be set with command line flag -k K, sorted in descending order of length.
An input command to boggle should look like:
$ java Boggle (-k [number of words])
(-n [width])
(-m [height])
(-d [path to dictionary])
(-r) < [input board file]Example
For input file test:
ness
tack
bmuh
esftwe expect:
$ java Boggle -k 7 < test
thumbtacks
thumbtack
setbacks
setback
ascent
humane
smacksFor input files test and testDict:
test:
baa
aba
aab
baadict:
aaaa
aaaaaOutput:
$ java Boggle -d testDict -k 20 < test
aaaaa
aaaaWarning: Do not use the StdIn class from the Princeton Standard Library. It's buggy and you might fail the autograder.
Timing and Runtime
You will be graded on runtime. You should be able to handle large dictionaries and boards efficiently. For a dictionary of fixed size and a random board, you should have runtime linear in the size of the board - that is, for an NxM board, your runtime should be expected O(MN).
I get the following results for timing:
hive19 [44] ~/proj3/src $ time java Boggle -r -n 100 -m 100 -k 10
unfeasible
...(more words)
real 0m0.582s
user 0m0.952s
sys 0m0.024s
$ time java Boggle -r -n 500 -m 500 -k 10
inexplicable
...(more words)
real 0m7.304s
user 0m9.569s
sys 0m0.393s
$ time java Boggle -r -n 500 -m 500 -k 400
...
real 0m7.277s
user 0m9.617s
sys 0m0.323s
$ time java Boggle -r -n 500 -m 500 -k 4000
...
real 0m7.341s
user 0m9.436s
sys 0m0.523s
$ time java Boggle -r -n 1000 -m 1000 -k 10
...
real 0m28.041s
user 0m36.419s
sys 0m0.566sYou should observe a similar order of growth (and runtime in general). On the lab machines your runtime should be within an order of 5.
Error Cases
For Boggle, throw an IllegalArgumentException (with some informative message of your choice) if:
- The input board is not rectangular.
- The dictionary file does not exist.
- N, M, or K is non-positive.
E. Submission
Submit the following files, any of their dependencies, and whatever tests you have written:
Trie.javaAlphabetSort.javaAutocomplete.javaBoggle.java(for gold points)
by pushing to submit/proj3.
For a single point of extra credit, push to ag/proj3 and pass over 50% of the ag tests by April 24th.
Please ensure that your code is reasonably within the style guidelines, and your methods and classes are well commented, explaining their implementations and runtimes.
For this project, a sanity checker will be running on the ag/branch and the full test suite will be on the submit/branch, once the tests are written.